用 TypeScript 实现斐波那契数列

发表于 | 更新于 | 分类于 | 阅读次数：

前几天在知乎看到一篇文章，用 TypeScript 类型运算实现一个中国象棋程序 ：

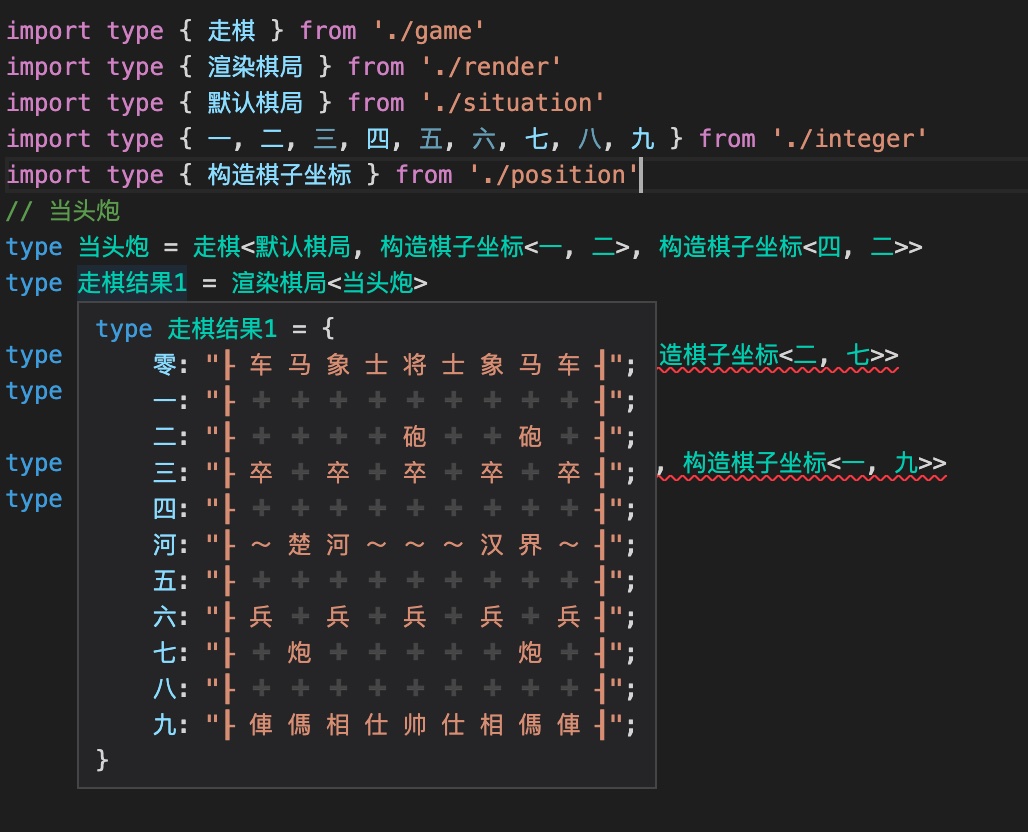
边看边 woc，TypeScript 不是一个类型系统吗，咋还实现象棋了，感觉发现了新大陆一样，然后把大佬的代码 clone下来，本地「运行」了一下，只能是带引号的运行了，因为 TS就是动态推导类型，只需要安装相关插件，鼠标 hover 上去就可以看到结果了。

看到这种神奇魔法，于是自己就查了查这是为什么。

图灵完备

这是接触到的第一个概念，维基百科是这样定义的：

一个计算系统可以计算任何图灵-可计算函数，被称作图灵完全（或者图灵完备）。或者任何可以模拟通用图灵机的系统。

可计算函数粗暴的理解为「人能计算的问题」，而现在例如 C++、JAVA几乎所有编程语言都是具有图灵完备性的，关于图灵完备是一个更大的问题，更通俗的解释可以看 什么是图灵完备？ 知乎这篇回答，很有意思，还了解到了一门有趣的编程语言 —— 1993 年Urban Müller 发明的Brainfuck 语言，感受一下它怎么打印 Hello World。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
+++++ +++++             initialize counter (cell #0) to 10
[                       use loop to set 70/100/30/10
    > +++++ ++              add  7 to cell #1
    > +++++ +++++           add 10 to cell #2
    > +++                   add  3 to cell #3
    > +                     add  1 to cell #4
<<<< -                  decrement counter (cell #0)
]
> ++ .                  print 'H'
> + .                   print 'e'
+++++ ++ .              print 'l'
.                       print 'l'
+++ .                   print 'o'
> ++ .                  print ' '
<< +++++ +++++ +++++ .  print 'W'
> .                     print 'o'

是的，你没有看错，左边是代码，右边是注释，这里 有运行的单句执行图示，可以感受一下：

上边的纸带代表内存中的情况，然后通过左移右移加加减减，最终输出了 Hello world!。

而在 TypeScript 仓库的一个 issues 中也讨论过 TypeScript 的图灵完备了，作者还分享了一个判断是否是质数的代码，也很有意思。

TypeScript 相关知识

为了实现文章的标题 「用 TypeScript 实现斐波那契数列」，需要先学习下相关的知识点。

泛型

如果之前学过 C++ 或者 Java 之类的语言，对泛型一定不陌生，泛型可以让我们定义函数参数的时候不指定参数类型，用一个占位符代替，当运行的时候再由外界传过来的类型决定。

举个简单的例子，实现两个元素相加，如果用 TypeScript 限制的话，即使是相同的逻辑也要写多次了。

1
2
3
4
5
6
7
8
9
10
function addTwoNumber(a: number, b: number):number {
  return a + b;
}

function addTwoNumberString(a: string, b: string):string {
  return a + b;
}

addTwoNumber(1,3)
addTwoNumberString('1', '2');

不然的话就只能 anyScript 了，完全失去了类型校验。

1
2
3
4
5
6
7
8
function addTwoNumber(a: any, b: any):any {
  return a + b;
}

addTwoNumber(1,3)
addTwoNumber('1', '2');

addTwoNumber('1', 2); //不报错

如果有泛型的话，就既可以达到逻辑的复用，同时对类型进行校验。

1
2
3
4
5
6
7
8
function addTwoNumber<T>(a: T, b: T): T {
  return <any>a + <any>b; //这里需要强制转换下，不然会报 Operator '+' cannot be applied to types 'T' and 'T'.ts(2365)
}

addTwoNumber(1, 3);
addTwoNumber("1", "3");

addTwoNumber('1', 2); //报错

当然上边有强行用泛型的嫌疑了，不过能大体理解泛型的作用就好，哈哈。上边的情况用 TS 的重载会更好些。

类型 type

TS 中除了基本的类型，number、string 、number[] 等，比较特殊的地方 1 、abc 、true 也可以单独算一个类型。1 的类型是 1，当然也属于 number。

最重要的是 TS 允许我们定义新的类型，而且我们还可以通过泛型变量，进行类型的运算然后产生新的类型。举几个例子：

1
2
3
type Type1<T> = T extends number ? number : string;
type Type2 = Type1<2121>; // 此时 Type2 就相当于 number
type Type3 = Type1<{}>; // 此时 Type3 就相当于 string

exstends 和后边的 ? 构成了一个三元表达式，如果 extends 前面的类型能够赋值给 extends 后面的类型，那么表达式判断为真，否则为假。

因为单个数字也是一个类型，所以我们就可以判断传入的 T 是否等于某个数。

1
2
3
type Type4<T> = T extends 1 ? true : false;
type Type5 = Type4<2121>; // 此时 Type5 就相当于 false 类型
type Type6 = Type4<1>; // 此时 Type6 就相当于 true 类型

可以仔细体会一下这里，很关键，后边写斐波那契数列的时候，一不小心就会被绕进去，因为我们是在操控类型之间的运算，和平时的编程感觉很不一样。

一句话总结，每个类型可以看成一个函数，传入的泛型是函数参数，并且也是一个类型，最后再返回一个新的类型。

1
Type(type, type) => type

infer

infer 表示在 extends 条件语句中待推断的类型变量。

简单理解，我们是为了判断某个类型是否 extends 某个「结构」，但结构中参数的类型我们并不知道，此时我们写一个 infer R（R只是占位，任何名字都可以），在类型推导的时候，R 就是当前类型真正的参数类型。举个例子：

我们判断 T 是否是 {a: XXX, b: XXX}的类型，因为 T 是泛型，我们并不知道T 中的 a 是什么类型，此时就可以用 infer 占位。当传入具体的类型是就可以拿到 a 是什么类型了。

1
2
3
4
type Foo<T> = T extends { a: infer U; b: infer U } ? U : never;

type T1 = Foo<{ a: string; b: string }>; // T1 类型为 string
type T2 = Foo<{ a: string; b: number }>; // T2 类型为 string | number

斐波那契数列

斐波那契数列就不多解释了，先用 js 实现一个斐波那契数列。

1
2
3
4
5
6
7
8
9
function Fibonacci(n) {
  if (n === 1) {
    return 1;
  }
  if (n === 2) {
    return 1;
  }
  return Fibonacci(n - 1) + Fibonacci(n - 2);
}

最关键的递归不用担心，TS 支持类型的递归定义，我们先写一个大概的雏形，看象棋直接用中文定义类型挺有意思，这里也直接中文了。之前总结的那句话这里再加深一下，每个类型可以看成一个函数，传入的泛型是函数参数，并且也是一个类型，最后再返回一个新的类型。

我们先定义「斐波那契」类型，泛型是传入一个数字（这里的数字是当作类型），先判断传入的类型是否是 1 或者 2，然后直接返回 1 类型。

1
2
3
4
5
type 斐波那契<某数 extends number> = 某数 extends 1 
  ? 1
  : 某数 extends 2
  ? 1
  : 相加<斐波那契<减一<某数>>, 斐波那契<减一<减一<某数>>>>;

上边需要注意的是 <> 里边的 extends 是为了限定传入的类型，和外边的 extends 不一样。

我们还需要定义一个「相加」类型和一个「减一」类型。

相加是两个类型相加，但是类型系统是不支持数字直接相加的，1 + 2 并不能直接相加，这里有个 trick。

数组类型和 js 中的数组一样，同样拥有 length 属性，返回一个具体的数字类型，也支持扩展运算符。举个例子：

1
2
type A = [any, any, any]
type B = A["length"] // B 就是 3 类型

所以我们可以将数字转为数组，操作数组，然后再将数组通过 length 转回数字。

先写一个得到对应数组的 Type，这里就需要用到递归了。

1
2
3
4
5
6
7
8
type 得到长度<数组 extends any[]> = 数组["length"];

type 转为数组<
  某数 extends number,
  对应数组 extends any[] = [] // 默认值赋一个空数组，外部调用的时候不需要传
> = 得到长度<对应数组> extends 某数 // 长度是否等于了需要的长度
  ? 对应数组 // 如果长度等于所需要的了就返回
  : 转为数组<某数, [any, ...对应数组]>; // 否则再添加一个元素进入数组，然后递归调用

有了转为数组的的 Type，相加方法就很好写了，我们只需要将两个数先转为对应的数组，将两个数组连接，最后返回连接后的数组长度即可。

1
2
3
type 相加<某数甲 extends number, 某数乙 extends number> = 得到长度<
  [...转为数组<某数甲>, ...转为数组<某数乙>]
>;

然后定义减一的方法，也就是数组长度减 1，这里就利用到了 infer，还需要利用数组的解构。

1
2
3
4
5
type 数组减一<某数组类型 extends any[]> = ((
  ...参数: 某数组类型
) => any) extends (拆一个元素: any, ...剩下的数组: infer 剩下的数组类型) => any
  ? 剩下的数组类型
  : [];

我们定义了一个函数类型，通过函数参数的解构，使得剩下的数组少了一个元素。

有了「数组减一」的类型，数字「减一」就水到渠成了，将数字转为对应数组，数组减去一个元素，然后恢复为数字即可。

1
type 减一<某数 extends number> = 得到长度<数组减一<转为数组<某数>>>;

整体代码就出来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
type 斐波那契<某数 extends number> = 某数 extends 1
  ? 1
  : 某数 extends 2
  ? 1
  : 相加<斐波那契<减一<某数>>, 斐波那契<减一<减一<某数>>>>;

type 得到长度<数组 extends any[]> = 数组["length"];

type 转为数组<
  某数 extends number,
  对应数组 extends any[] = []
> = 得到长度<对应数组> extends 某数
  ? 对应数组
  : 转为数组<某数, [any, ...对应数组]>;

type 相加<某数甲 extends number, 某数乙 extends number> = 得到长度<
  [...转为数组<某数甲>, ...转为数组<某数乙>]
>;

type 数组减一<某数组类型 extends any[]> = ((
  ...参数: 某数组类型
) => any) extends (拆一个元素: any, ...剩下的数组: infer 剩下的数组类型) => any
  ? 剩下的数组类型
  : [];

type 减一<某数 extends number> = 得到长度<数组减一<转为数组<某数>>>;

// 测试
type 斐波那契八 = 斐波那契<8>

看下结果：

不过到斐波那契 11 就因为递归层度太深 gg 了。

这里主要就是体验下 TS 的图灵完备，优化就不考虑了。

总结

通过写一个这个例子对 TS 的类型有了更多的了解，但平时开发肯定不会这样搞，主要是写着玩哈哈，毕竟一个简单的斐波那契数列都写的这么麻烦，引用 Linus Torvalds 自传的书名结束吧，Just for Fun！

windliang wechat