Sigmoid 美 [‘sɪgmɔɪd] : S 形的
Discriminative 美 [dɪ’skrɪməˌneɪtɪv] : 判别
本文是对李宏毅教授课程的笔记加上自己的理解重新组织，如有错误，感谢指出。
视频及 PPT 原教程：https://pan.baidu.com/s/1brbb6rX 密码：ty1r
接着上篇的生成模型，我们进行下公式的变形，见证奇迹的发生！
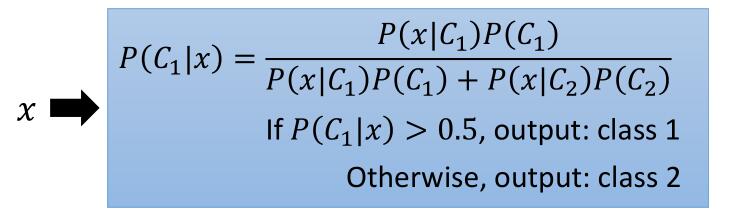
问题的关键是求出 P( x | C1) 和 P( x | C2)，我们对它们的分布做出假设，用贝叶斯或者高斯分布最终求出了 P( x | C1) 和 P( x | C2)，从而解决了我们的问题。而在这里我们先对公式进行一下变形。
exp( -z ) 代表 e 的负 z 次方
最终的结果其实就是 S 型函数，即 Sigmoid function ，记为 $\sigma(z)$ 。
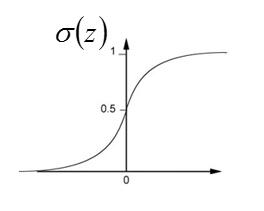
我们再来看一下 z 长什么样子。
为了方便推导，我们依旧假设 P( x | C1) 、P( x | C2) 符合高斯分布，并且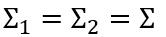 
当然如果假设它是别的分布，最终依旧可以推导出同样的公式。
经过代入、合并、化简，它变成了下边的样子。
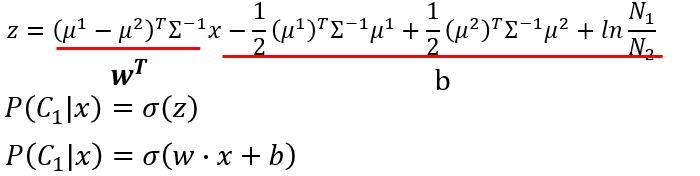
仔细观察，我们可以把 x 前边的系数记为一个向量 w , 而后边的一大串其实这是一个标量，一个常数项，我们记为 b 。
因为假设不同的分布最终都可以得到这个式子，所以我们如果对 w 和 b 直接求解，求得的 w 和 b 就可能是任何一种分布， 它可以是高斯分布，可以是贝叶斯，甚至是一些没有命名的分布。
而这个模型就是 LR ( Logistic Regression )，也是判别 ( Discriminative ) 模型的一种。虽然和生成模型经过变化长一个样子，但由于求参数方式的不同，最终的效果也不一样。
判别模型中我们直接求 w 和 b （当然是梯度下降的方式，后边我们进行推导），生成模型中我们先假设一种分布，然后再往出推导公式从而算出 w 和 b。
区别很容易理解，判别模型中我们直接求出 w 和 b ，此时代表的分布并不是确定的，可能是贝叶斯，可能是高斯或者其他。而生成模型开始假设什么分布它就是什么分布。
很明显，判别模型在大多数情况下会优于生成模型，因为生成模型需要人为的假设分布，一旦假设错了，它的 w 和 b 即使求的再正确，最终结果也不会太好。
生成模型就没有什么好处了吗？ 当然是有的
如果我们的数据很少，而此时我们先假设一个分布再去求，最终效果肯定会比判别模型中盲目的求要好。
如果数据的噪音比较多，也就是很多错误的数据，如果我们开始假设了分布，这些噪声对模型不会造成太大的影响，这种情况下它更鲁棒 ( 稳定、健壮 ) 些。
说了这么多，那么我们如何求 w 和 b 呢？
下边进入我们熟悉的流程 Model → Goodness of a Function → Find the best function 。
Model
再强调一下，忘掉我们怎么推出的这个模型，它和高斯分布没什么关系，即使假设其他的分布依旧会推出下边这个模型。现在我们的重点是如果有了这个模型，怎么去求 w 和 b 。
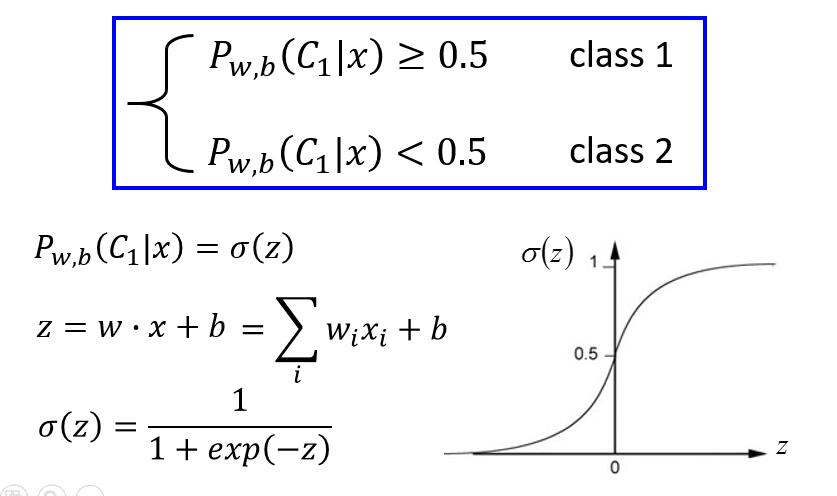
阙值可以选 0.5 ，也可以选其他，具体看问题需要。
换一种画法
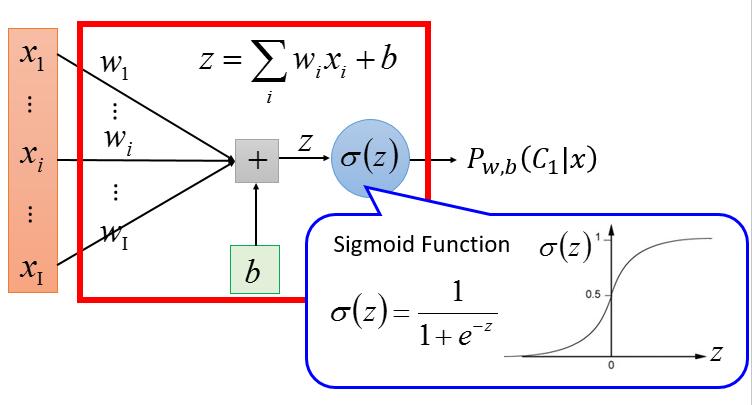
Goodness of Function
看下我们的数据
此时我们的输出是 C1 、C2 ，首先我们得把它数值化，我们假设 C1 是 1，C2 是 0 。
有了这些数据，有了模型，我们先假设所有数据其实是从下边这个模型（LR）得到的。
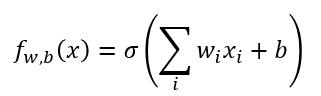
记得线性回归中的 Loss function 怎么定义的吗？我们是不是也可以这样做呢？
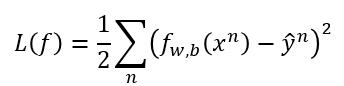
很可惜，不可以，此时的 L 不是一个凸函数，局部最优值太多了，根本没法去梯度下降，所以我们得找其他的 Loss Function 。
这里我们假设原来的每一个数据是一个伯努利分布，也就是我们熟悉的两点分布。
我们假设这样一个事件，假设一个随机变量是 Y ，数据属于 C1 类记为成功，记做 Y = 1 ，如果不属于 C1 类记为失败，记做 Y = 0 。
这样的话，所有数据都可以统一为一个式子 , n 代表第几个数据：
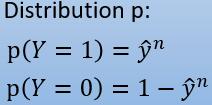
而我们的模型算出的每个数据的概率，也可以统一为一个式子：
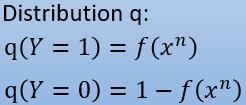
如何让分布 q 尽可能的接近分布 p 呢？让他们的交叉熵最小！交叉熵的概念可以看下知乎里的讨论。交叉熵的公式如下：
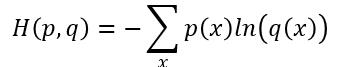
x 这里指的是 Y 的取值。
然后对于每一个数据的交叉熵是
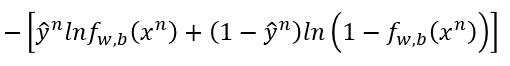
我们再把所有的交叉熵求和，就是我们的 Loss Function 了。
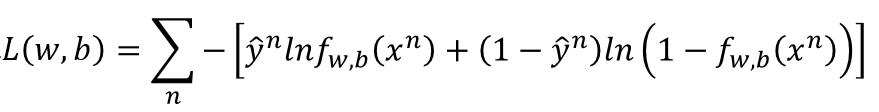
我们再换种思路求 Loss Function , 即用最大似然估计的方法，也就是利用所有的数据，找到一组参数使得数据尽可能的符合模型。假设我们的分布如下
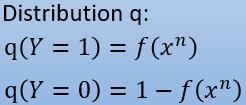
最大似然估计就是把每个样本带进去，然后乘起来，也就是
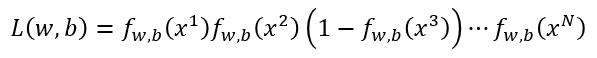
我们需要做的就是找到 w , b 使得这里的 likelihood 最大。
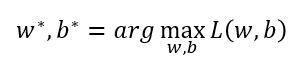
我们把 L 取一下自然对数，然后添一个负号，求最大变成求最小。
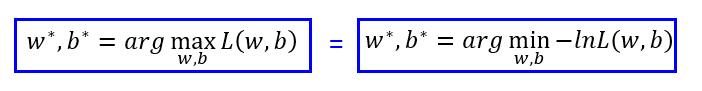
接下来进行化简，把 L 代入，ln 里的拿出来乘法变加法
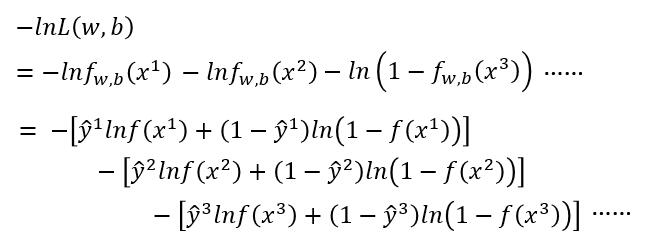
神奇的第二个等号后边的变化是怎么回事呢？其实我们利用了数据
我们把 $\hat{y}^1 , \hat{y}^2 , \hat{y}^3$代入就可以反推回第一个等号后边的式子了。
然后我们把式子合并就变成了下边这样
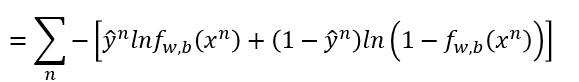
是的，你没有看错，我们得到了和之前用交叉熵推出的一样的公式！！！究竟是道德的沦丧？还是人性的缺失？让我们一起来走近科学。
Best Function
让我们看下对 wi 求偏导， b 就先不看了。
所以我们的 wi 的更新方式就是
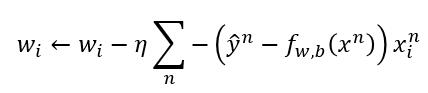
有了参数的更新方式，下边就不用讲了吧，嘻嘻嘻。
与线性回归对比
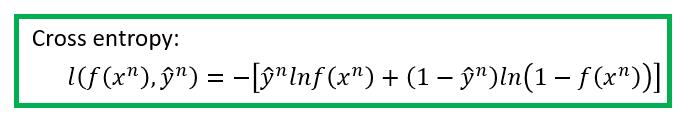
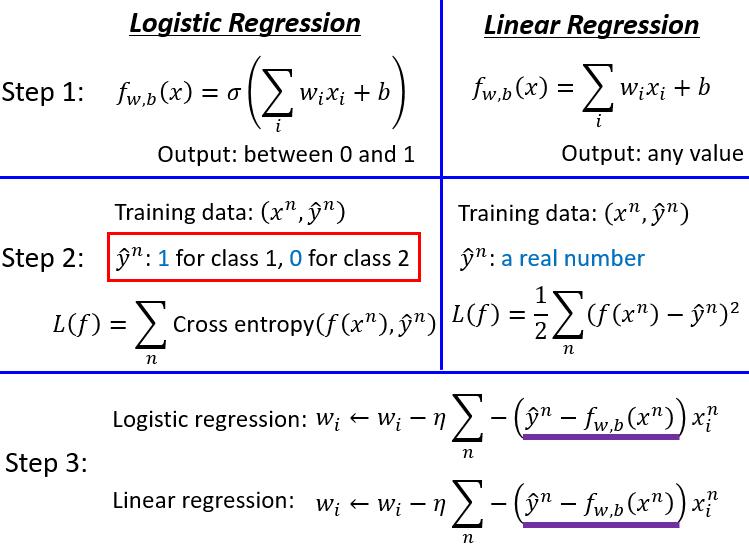
神奇之处又来了，梯度下降参数更新的公式竟然一样！！！究竟是道德的沦丧？还是人性的缺失？让我们一起来走近科学。
