Generative 美 [ˈdʒɛnərətɪv, -əˌre-] : 能生产的,有生产力的; 生殖的;
Model 美 [ˈmɑdl] : 模型
likelihood [ˈlaɪkliˌhʊd] : 似然函数
Maximum 美 [ˈmæksəməm] : 最大值
features 美 [‘fitʃəz] : 特征
vector 美[ˈvɛktɚ] : 向量
matrices 美 [ˈmetrɪˌsiz, ˈmætrɪ-] :矩阵
本文是对李宏毅教授课程的笔记加上自己的理解重新组织,如有错误,感谢指出。
视频及 PPT 原教程:https://pan.baidu.com/s/1raoObGo 密码:31cw
前边我们讲的线性回归模型主要做预测,而这里的 Generative Model 则主要用于分类问题。
问题提出
同样我们以神奇宝贝为例,进行分类。

假如我们有以下的数据
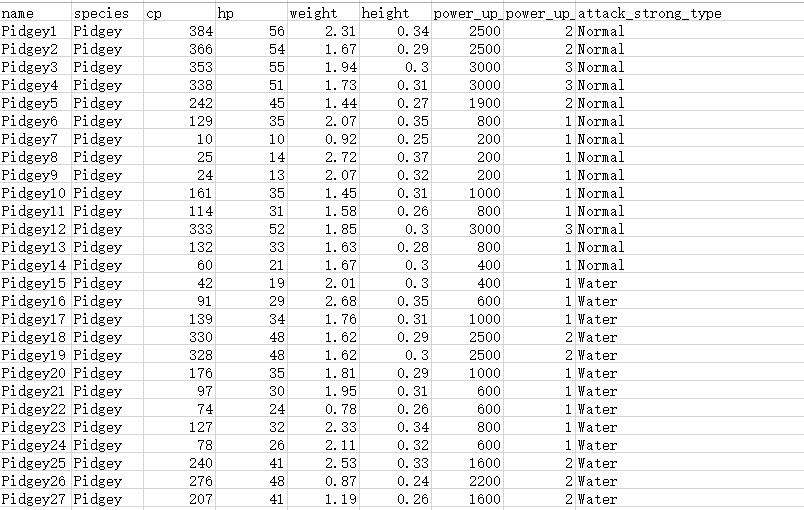
假如我们有 79 只 Water , 61 只 Normal 。
为了问题的简单化,我们假设神奇宝贝的 attack_strong_type 只有两类,一种是 Normal,一种是 Water。我们先选取它的两组属性 Defense 和 SP Defence(图中未显示) 来预测它是属于 Normal 还是 Water。也就是说每一个个体可以由一个向量表示:

我们需要找到一个 f ,把 x 输入即可输出 x 属于哪一类,Class1 ( Water) 还是 Class2 ( Normal )
Model
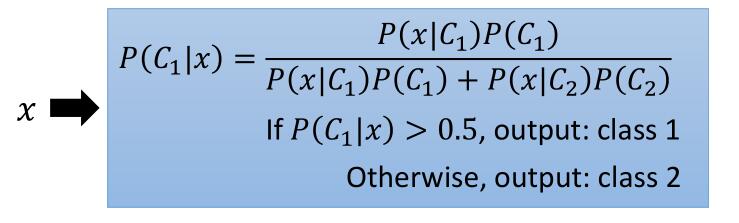
P(C1) 代表属于 Class1 的个体占整个样本比例。
P(C1 | x) 代表 x 属于 Class1 的概率。
这个公式其实是贝叶斯公式和全概率公式的结合,具体讲解可以看阮一峰老师的推导,非常通俗易懂。
为什么大于 0.5 就是 Class1?否则就是 Class 2。
因为这个问题是二元分类,如果 P(C1 | x) 大于 0.5 那么 P(C1 | x) 一定大于 P(C2 | x) ,所以我们判断当前 x 属于 Class1。反之同理。
如果是多元分类该怎么办?
把 P(C1 | x)、P(C2 | x)、P(C3 | x)、P(C4 | x)……每个概率都算出来,哪个大就说明它属于哪一类。
观察到公式 P(C1) 和 P(C2) 非常好算,无非是用属于 Class1(Water) 的个体数量处除以总数就是 P(C1),用属于 Class2(Normal) 的个体数量处除以总数就是 P(C2)。如下图:

真正的问题是 P( x | C1)怎么进行计算?也就是 P(SP Defense, Defense | C1 ) 怎么计算?
第一种解决方案就是假设 SP Defense 和 Defense 是独立的,然后 P (SP Defense , Defense | C1) = P(SP Defense | C1) · P(Defense | C1) ,利用这个公式和所有数据我们就可以把每个数值都算出来了。这就是朴素贝叶斯分类器,具体还是看阮一峰大神的博客。
第二种解决方案我们就假设每一类都是一个高斯分布(正态分布)。什么意思呢?
我们先从一维的高斯分布理解。

假设某正态分布的概率密度分布图如下:
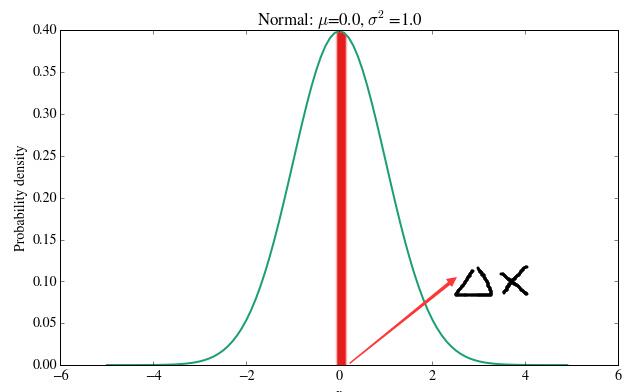
那么变量等于 0 的概率密度是 0.4 ,那它的概率是多少呢?理论上某个点的概率应该是 0 ,但我们可以求 (0 , 0 + △x) 的概率,那么 (0 , 0 + △x) 的概率可以近似于红色矩形的面积,所以 (0. , 0. + △x) 的概率就是 0.4△x。假如 △x 很小,那么我们就可以近似的把 0 处的概率当做 0.4△x 。
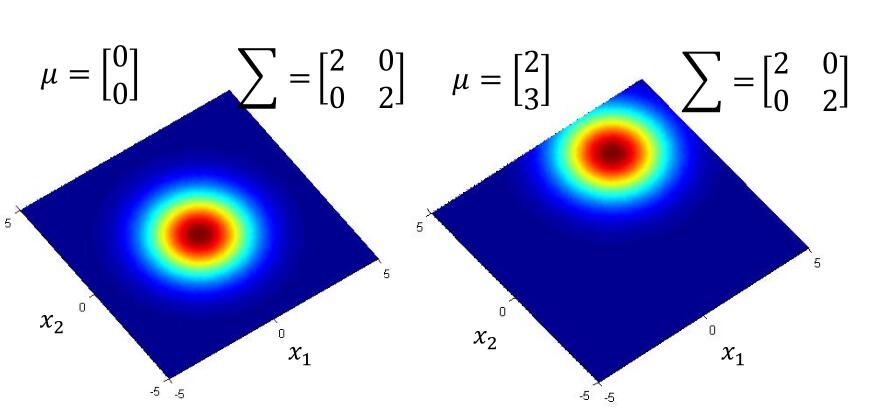
同理,我们再看二维的高斯分布。
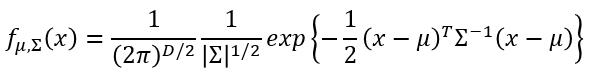
它有三个参数。
如果 x 是 n 维向量,那么D = n ( 相当于常量 ), $\mu$ 是 n 维向量, $\Sigma$ 是 n × n 矩阵。
我们看一下 x 是二维的它的概率密度分布图。
而如果求某一点 x 的概率,则可以类似于一维高斯下,近似表示为
$$f_{\mu,\Sigma}(x) \cdot (\Delta x)^2 $$
所以我们的模型就变成了
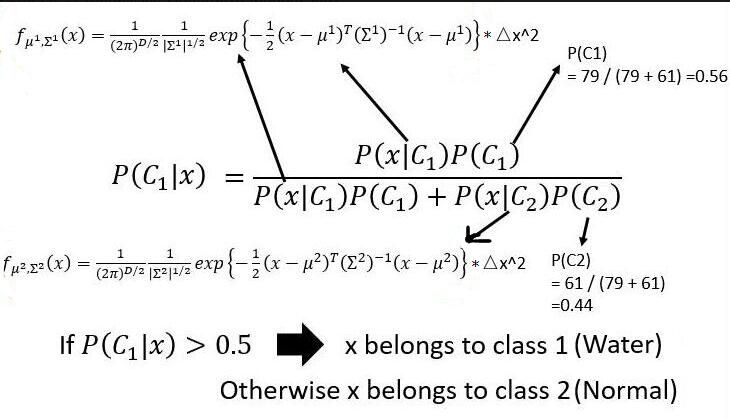
然后我们可以把 $(\Delta x) ^2$ 约掉,就变成了
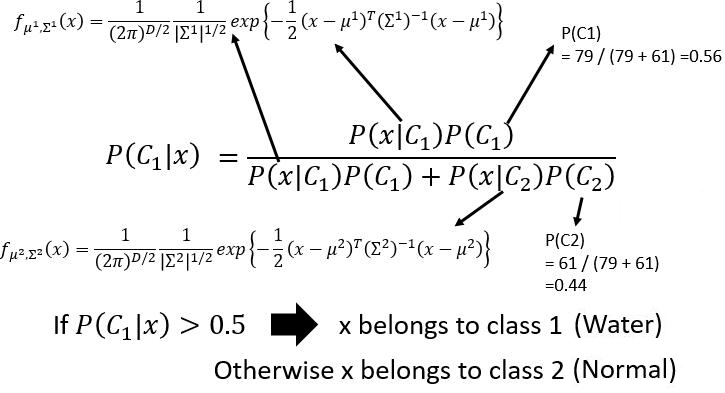
所以我们的问题变成了如何选取一个好的 $\mu ^1 , \Sigma ^1 , \mu ^2 , \Sigma ^2$ 。
Goodness of Function
这一步我们来求解最好的 $\mu ^1 , \Sigma ^1 , \mu ^2 , \Sigma ^2$ 。
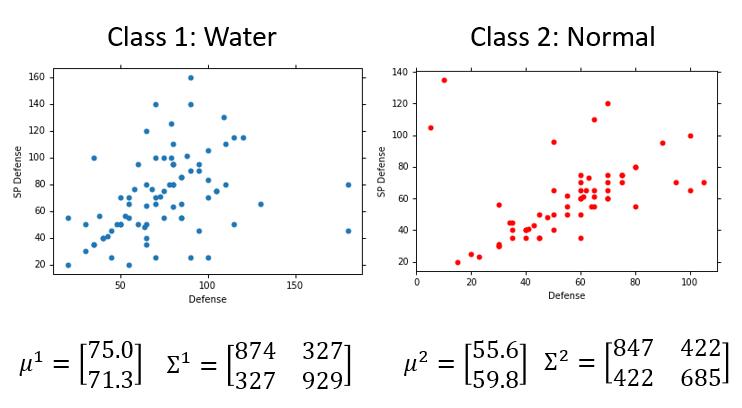
我们先分析 Water 类的,即求 $\mu ^1 , \Sigma ^1$。我们把每个样本画到图中。
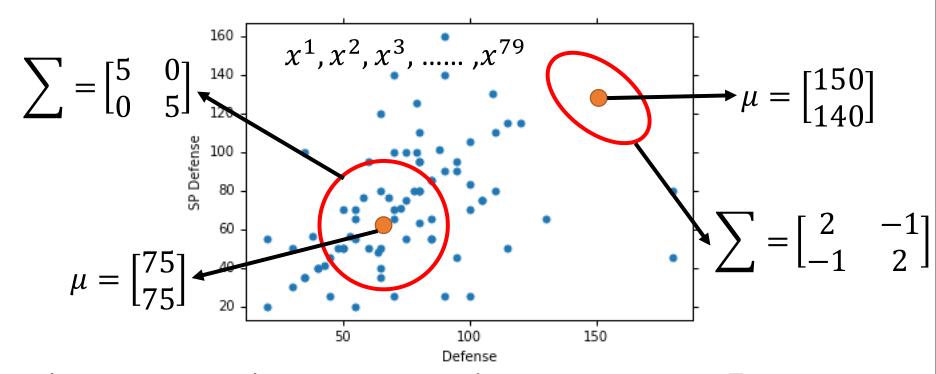
我们可以看到 $\Sigma , \mu$ 取不同的值,假如一个圆圈代表一个高斯分布,每个点的概率将会不同,而我们的目的是让所有点的尽量符合当前模型。此时,我们可以用一个 likelihood ( 似然函数 ) 来衡量。
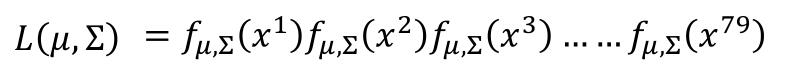
我们的目的就是找一个 $\Sigma , \mu$ ,使得 likelihood 达到最大,也就是最大似然估计。即
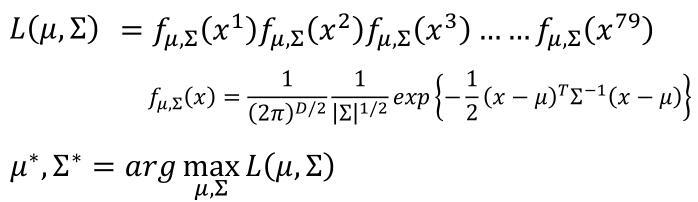
Best Function
根据统计学的知识,我们可以直接求出 $\mu$ 和 $\Sigma$。
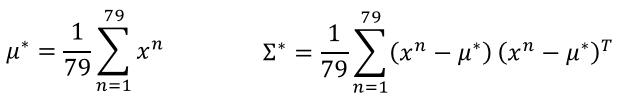
利用公式
我们最终得到的模型就是

这样我们就可以愉快的做分类了。
Test & 重新设计模型
经测试,我们的正确率只有 47% 。
难道是我们的维数太低,我们只选取了 SP Defense , Defense 两个 features,如果我们选 hp , att , sp att , de , sp de , speed 6 个 features 呢?此时

然而准确率依旧没有怎么提高,变为了 64% 。
我们针对高斯再进行一下优化。
之前我们有四个参数,$\mu ^1 , \Sigma ^1 , \mu ^2 , \Sigma ^2$ ,我们可不可以把 $\Sigma ^1 , \Sigma ^2 $变为一个,变为 $\mu ^1 , \Sigma , \mu ^2 $ 三个参数,简化我们的模型。
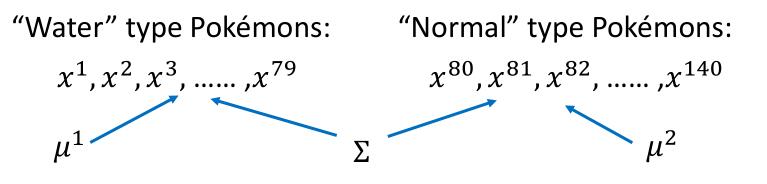
我们计算的公式将变成
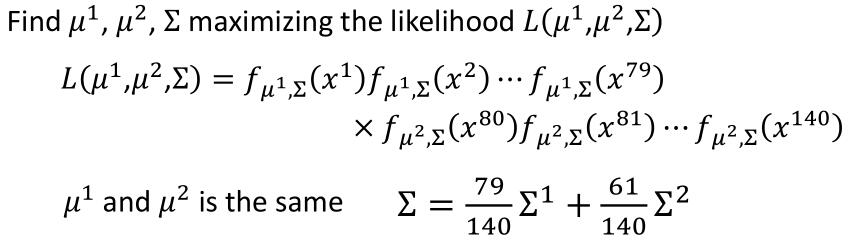
然后我们的模型变成了
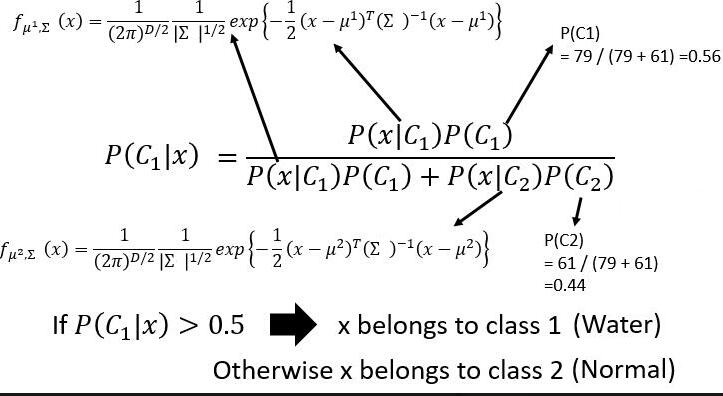
此时,我们的正确率变为了 74% ,有了很大的提高!
总
类比于线性回归,我们依旧是先提出模型,然后提出计算参数的公式,最后对数据进行测试,继续完善我们的模型。
