tuning 美 [‘tjunɪŋ] : 调整
learning rate 美[ˈlɚnɪŋ ret] : 学习速率
stochastic 美 [stə’kæstɪk]:随机的
batch 美 [bætʃ] : 一批
dimension 美 [dɪˈmɛnʃən, daɪ-] : 维度
mean 美 [min] : 平均数
standard deviation美 [ˈstændəd ˌdiviˈeʃən] : 标准差
variance 美 [ˈveriəns] : 方差
本文是对李宏毅教授课程的笔记加上自己的理解重新组织,如有错误,感谢指出。
视频及 PPT 原教程:https://pan.baidu.com/s/1bSs66a 密码:g8e4
上篇详细介绍了梯度下降,这篇讲一下对梯度下降的一些优化。
Tuning your learning rate
Adagrad
下边是梯度下降的公式。
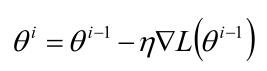
这里的 $\eta$ 是一直固定不变的, 而直观上,我们开始离目标点远,$\eta$ 值应该大一些,随着迭代的进行,我们离目标点越来越近,$\eta$ 值应该变小。所以我们得到了第一次优化的版本:
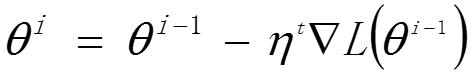

t 代表迭代的次数。
还存在一些问题,就是这里的 $\theta$ 代表一组参数,也就意味着我们对不同的参数使用了同一个 $\eta$ 。而每个参数对 Loss 值影响不一定相同,所以我们如何让不同的参数拥有不同的 $\eta$ 呢?
因为每个参数的偏导值肯定是不一样的,我们不妨在上边优化的基础上再除以关于他们偏导值的东西,除以之前迭代的所有导数的平方的平均数再开根号。下边的 w 代表一个参数,其他参数同理,t 同样代表迭代次数。
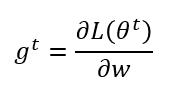

我们把它和上边的优化综合在一起
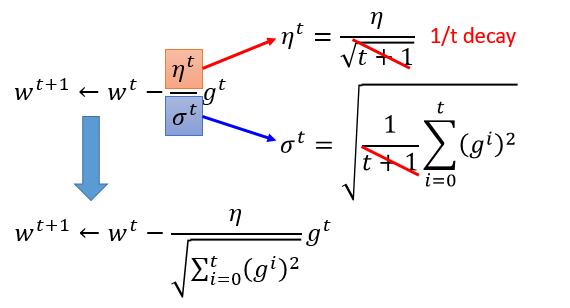
这样我们就得到了 Adagrad 的公式,即 $\eta$ 除以之前迭代的所有导数的平方的平均数再开根号,而迭代次数已经被我们约掉了。
Adagrad 原理
我们简单的理解一下它的原理。

我们假设 Loss Function 是 y ,对称轴是 - b / 2a ,初值选取了 $x_0$ ,而此时 Best step 如图所示,也就是 $x_0$ 减去它就到了最小值,让我们和 Adagrad 对比一下。
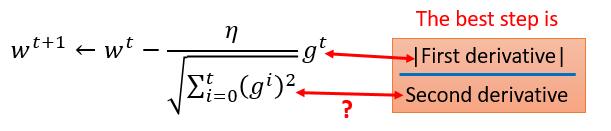
是的, Adagrad 的想法就是除以一个可以近似代表二次导数的东西,当然我们也可以直接除以二次导数,但那样对于复杂的函数会增加很多计算量。
除了 Adagrad ,还有很多方法都是针对 $\eta$ 进行优化。
Stochastic Gradient Descent (随机梯度下降)
我们举一个简单的例子,就是前边文章的预测神奇宝贝进化后的 cp 值,假如 Loss Function 是下边的
$$ L = \sum_{n=0}^{10} ( \hat{y}^n - ( b+ w · x{^n_{cp}} ) )^2$$
我们总共有 10 组已知的数据,$x^n$ 代表第 n 只神奇宝贝进化前的 cp 值,$\hat{y}^n$ 代表第 n 只神奇宝贝进化后的 cp 值。我们计算 Loss 的时候把所有的数据全部用到了。
我们如果计算 Loss 的时候不用全部的数据会怎么样呢?也就是我们每次只随机或者顺序选一只神奇宝贝,即 Loss Function 如下:
$$ L = \hat{y} - ( b+ w · x{_{cp}} ) ^2$$
这样我们根据其中一个数据直接算 Loss Function 的偏导,利用梯度下降进行更新参数就叫做 Stochastic Gradient Descent 。这样做的好处是可以更快的收敛,它的效果图可能如下:
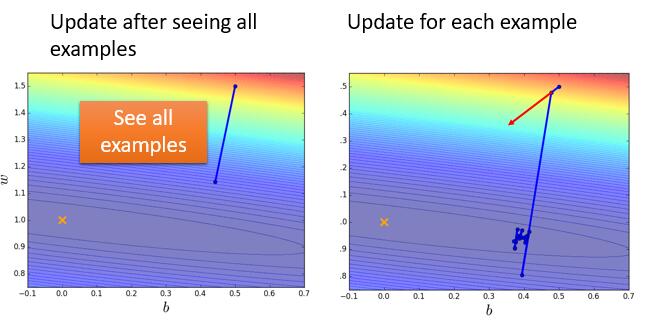
10 组数据左边的图只更新了一次,而右边的图就更新了 10 次。
同理如果我们每次同样不选全部数据,而是选择部分数据,例如每次全部数据的十分之一,这样再进行梯度下降,就又是一个新的优化方法,叫做 mini-batch gradient decent , 小批的梯度下降。batch_size 就代表每次选择多少数据。这种方法用的最多。
而我们一开始使用全部数据的更新方式叫什么呢?Batch gradient descent ,批梯度下降。这种方法每更新一次参数都要把数据集里的所有样本都看一遍,计算量开销大,计算速度慢,不常用。
Feature Scaling
简单的讲,就是把所有参数的取值范围统一到一个范围,如下图。
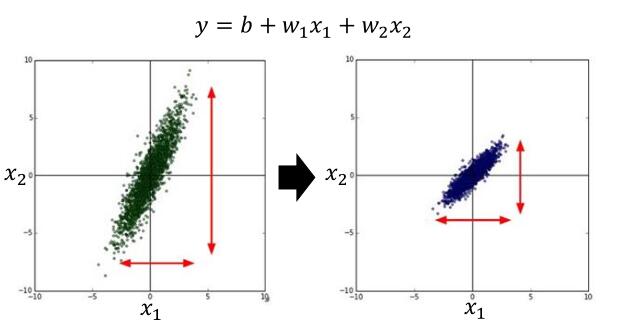
为什么这样做呢?我们把上边的 y 函数用另一种图示表示。

$x_1$ 的取值是 1,2…… , $x_2$ 的取值是 100,200 ……
y 代表 Loss Function ,我们往 $w_2$ 的方向看,等高线比较窄,说明 $w_2$ 的变化对 L 的影响大。而看横轴 $w_1$ 的方向比较稀疏,说明 $w_1$ 对 L 的影响小。这显然是不合理的,每个参数对 L 的影响应该同等才可以,我们应该达到下边的效果:
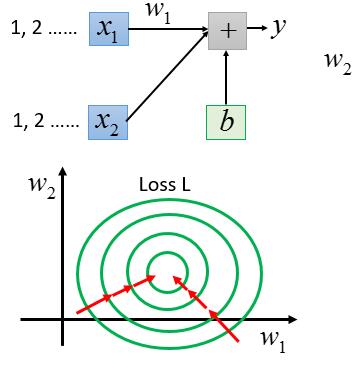
这样做的好处很明显,每次参数的更新会直接朝向目标值,而不会向之前每次更新的方向都不同。
那么具体怎么操作呢?

把样本每一维度的参数减去平均值 $m_i$ 除以标准差 $\sigma_i$ 即可。
最后会使得每一维度参数的取值的平均值为 0 ,方差为 1 。
