之前写了 进制转换,也写了计算机怎么 存整数,那么问题来了,计算机中小数怎么存呢?比如2019.725怎么放到计算机里呢?-2019.725又该怎么办呢?
我们有什么
首先想一下我们有什么,计算机怎么存数。假如我们的计算机是存 32 位的,那么它就长下边的样子。

由于我们写数字,习惯于先写高位,所以把最低位画到了最右边。
我们需要做的就是把0和1放到上边的方框中,来表示2019.725。换言之,我们就是需要制定一个规则,把2019.725转成01字符串存进去。然后读取的时候,再把01字符串转成2019.725显示出来。
思路一
简单粗暴些,我们人为的把32个位置分成三部分,最高位0表示正数,1表示负数,然后是整数部分,再然后是小数部分。

低 10 位存小数部分,接下来的 21 位存整数部分,最高 1位存符号位。所以我们只需要把2019和725分别转成二进制,放进去就可以了。二进制位数不足的,高位补零就可以。
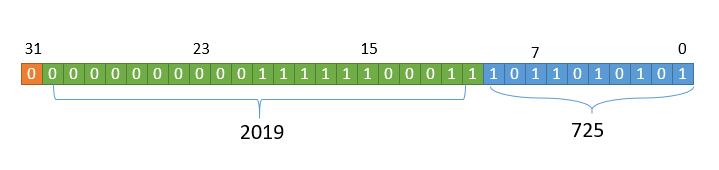
仔细想想,规则还不够完善,如果存10.3和10.03,小数部分怎么存呢?肯定不能都存3,这样两个数就不能区分了。这里我想到两种方案:
倒序
小数部分我们逆转以后去存,10.3小数部分存3,10.03小数部分存30。
补零
我们的小数部分是10个比特位,所以最多存 $2^{10}$ 个数,十进制的话就是0 - 1023。为了方便,把1000以上的数省略掉,范围变成000-999,也就意味着我们能精确的表示小数点后三位的数,如果一个数小数位数不足3位,我们就用零补齐。
10.3的话,可以看成10.300,小数部分存300,10.03的话可以看成10.030,小数部分就存30。
能表示的数字范围
整数部分我们有21个比特位,能表示的数是 $2^{21}$ 个,十进制的话就是 0 - 2097152。
小数部分如果用的倒序方案,那么我们的范围就是0 - 1023。
综上,数字范围就是 -2097152.1023 ~ 2097152.1023。
应用
MySQL 中的定点数DECIMAL就是采取的上边的思想,将整数部分和小数部分分别存储。不同之处是MySQL采用了变字长存储,根据十进制的大小,利用不同的字节去存储,所以理论上它能存的范围是无限的。
详细的介绍可以参考 你可能不知道的MySQL中的定点数类型。
思路二
上边的方案有一个问题,表示的数字的范围有些小,最大也才两百多万。限制范围的原因就是,上边的方案整数部分只用了21个比特位去存。
换一种思路,我们通过移动小数点把小数转成整数,然后再记录小数点移动的位数。
我们用3个比特位来记录移动的位数,这样我们就可以把小数点移动7位。此外,整数部分就可以有28个比特位来表示了,范围大大增加。

其实可以看做是科学计数法的形式,比如2019.725,可以看做是 $2019725\times10^{-3}$,我们只需要把 2019725和指数3存起来就可以了。

能表示的数字范围
28个比特位来表示整数部分,能表示的数的个数就是 $2^{28}$,对应的十进制范围就是0 - 268435455。
又因为最多可以移动 7 位的小数,所以数字范围就是下边的
-268435455.0000000 ~ 268435455.0000000。
可以看到比之前的方案扩大了两个数量级,精度也提高了。但是我们要意识到一件事情,两种方案都用了32个比特位,所以最多就是表示 $2^{32}$ 个数。思路二表示的范围虽然扩大了,并不是这个范围内的所有数都能精确表示,能表示的数的范围是0 - 268435455,也就是能表示的有效数字最多只有九位。
对于思路一的最大数2097152.1023,如果用思路二,虽然它在-268435455.0000000 ~ 268435455.0000000之内,但是由于它的有效数字位数是11位,但我们最多存储9位的,所以我们只好把小数点后的最后两位舍去,存储2097152.10。
应用
对于C#中的System.Decimal是用的类似于思路二的思想,具体的话参考 没有神话,聊聊decimal的“障眼法”。
思路三
上边的思路一和思路二都是站在十进制数的角度上先考虑对数字的分割、转换,然后将十进制的整数转为二进制进行存储的。再换一种思路,先把十进数转成二进制数,再去存呗。
对于2019.725转成二进制就是11111100011.1011100110...,为啥出现了省略号?进制转换中已经讨论过这个问题了,那就是大部分十进制数并不能精确的转到二进制,这是一个固有的事实,我们也没啥办法,假装没有省略号,继续讨论吧。
尾数部分
这里存储的话,可以借鉴思路二,我们可以把二进制小数转换成科学计数法的形式,统一规格再去存储。这里用个小技巧,我们知道所有的数字除了0之外,一定会含有一个1,所以我们把数字转成下边的形式。
$$1.xxxxxxx…\times2^{E}$$
为什么要用上边的形式呢,这样做的一个好处就是存的时候,我们只需要存xxxxxxxxx...的部分,显示数字的时候再考虑它的最高位还有一个1。这样如果用23个比特位来存数字,相等于存储了24位。
指数
区别于思路二的指数,思路二我们是把原来的小数转为整数,所以指数一定是个负数,直接存它的绝对值就行。但在这里如果之前的数字是 0.000001这样的,那么指数E是负数,但如果是1110011.1这样的,指数E就是正数了。
如果指数E是用8个比特位来存储,那么总共就是 $2^8$ 个数,范围就是0 - 255,那么怎么存负数呢?最简单的方案,人为规定呗,将一部分正数映射到负数上,就对半分吧。
1 | 0 1 125 126 127 128 129 254 255 |
要表示的指数加上127映射到0 - 255。反过来显示指数真正值的时候,需要减去127。
综上所述,我们就用 1 个比特位来存符号位,8个比特位来存指数,存的时候记得加上偏移,剩下的23个比特位来存有效数字,而事实上我们其实可以看做存了24位。

这样的话,求出2019.725的二进制是 11111100011.1011100110011。把它规格化,小数点需要向左移动10位,也就代表指数是 10,存的话还需要加上127,也就是137了,二进制表示是10001001。所以规格化就是下边的数了:
$$1.11111000111011100110011\times2^{10001001}$$
所以计算机中就是下边这样存的了。

特殊数字
我们还有个问题没有解决,上边规格化的时候我们默认了所有数字至少有一个1,但是0怎么办呢?规则是我们自己定的,继续定呗。
当指数是-127时,一个很小很小的数了,此时对应的指数加上127,也就是0。我们规定当E为0并且M全为0,我们就说这个数字是0。
-127用了以后,负指数最小就是-126了。
让我们再规定几个特殊的数字。
当指数是128时,一个很大很大的数,也就是当 E 全为1。分几种情况。
有效数字
M每一位全为0,S为0,就代表正无穷。S为1,就代表负无穷。
有效数字 M 每一位不全为 0,代表
NaN,表示不是一个数字。
所以此时正指数最大就是127了。
能表示数的范围
最大数和最小数
最大的数,指数最大取1111 1110,也就是254,减去127,代表指数是127。有效数字全部取1,也就是1.111...1,小数点后边23个1。然后把它转成十进制的话,用一个技巧,先给它加 $2^{-23}$,这样所有的1都产生进位,变成了10.0000000,这样的话转成十进制就是2了,当然我们还要减去 $2^{-23}$。
综上,最大的数字用十进制表示就是 $(2-2^{-23})\times2^{127}$,也就是 $3.4028234663852886\times10^{38}$。
所以能表示的范围就是 $-3.4028234663852886\times10^{38}$ 到 $ 3.4028234663852886\times10^{38}$。
再看一下能表示的最小正数。指数取最小为 0000 0001,减去127,代表指数是-126。有效数字全部取0,其实也就代表1.000...0000,总共有23个0,转成十进制的话就是$1\times2^{-126} $,也就是 $1.1754943508222875\times10^{-38}$。
有没有发现一个问题,我们要找最小的数,但因为之前的规定,最高位却能是1。但理论上我们找一个0.000...1这样的数才代表最小的正数。怎么得到这样的数呢?
再加个规则吧。当时我们规定当E为0的并且M每一位全为0,我们就说这个数字是0。那M不全为零呢?
之前是假设省略了最高位1,我们加一个新规则,当E全为0时,我们就说最高位不再省略1。所以最小的尾数就可以是0.00...1了,小数点后22个零,转成十进制就是 $2^{-23}$。指数还是之前的-126,所以比之前更小的正数就是 $2^{-23}\times2^{-126}=2^{-149}$,也就是 $1.401298464324817\times10^{-45}$。
精度
我们用23个比特位表示尾数部分,最多能表示 $2^{23}$ 个数,也就是8388607,从十进制的角度,所以它的有效数字最多有7位。
应用
上边介绍的其实就是IEEE 754标准了,计算机中存储32位浮点数基本上都是这个规则。比如java中的float类型,可以看一下jdk源码中的一些定义。
1 | /** |
可以看到float的最大值,和正数的两个最小值和我们分析的完全一致。
当然,上边的我们分析的是32位的情况,64位的话和32位基本是一样的,对应于java中的double类型。
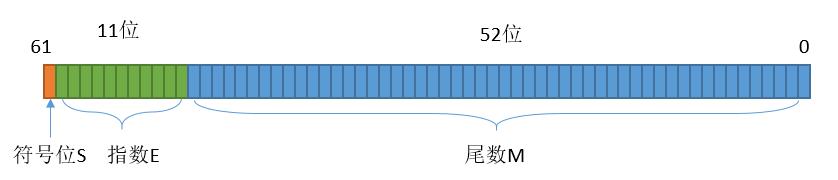
除了位数变多以外,其它的分析和32位都是一样的,此时指数不再加127,而是加1023。
一些问题
1 | 0.1 + 0.2 == 0.3 //false |
这样就可以理解上边的经典问题了,之所以两边不相等,第一个原因就是大部分十进制并不能精确的转为二进制,第二个原因就是存储的位数有限,会进行一些舍去。
如果对于一些能精确表示的浮点数,判断相等就不会出问题了。
1 | 0.125 + 0.125 == 0.25 //true |
另一个问题,当我定义一个变量
1 | float a = 0.1; |
既然不能精确表示0.1,那么我们把它输出的时候为什么显示的是0.1。
在 进制转换 中我们算过,0.1 转成二进制的话是0.0 0011 0011 0011...,因为我们只能存23位有效数字,所以我们只能存0.000 1 1001 1001 1001 1001 1001 101。
因为我们最高位可以省略个 1,所以就是第一个1后边有23位。
此外,最后 3 位本来是100,因为100后边一位是1,所以相当于产生进位变成101。
这个二进制数还原为10进制的话就是0.10000000149011612。
让我们来验证一下
1 | System.out.println(String.format("%.18f", 0.1f)); |
和我们预想的完全一样,而如果不加限制直接输出0.1,显示0.1只是因为默认的有效位数比较少,其实只是输出了近似值0.1。
结束
浮点数的探究到此结束了,回顾一下,前两种方法我们先从十进制的角度来考虑,通过存整数来存小数,从而保证了我们可以精确存数。思路三,我们先把十进制转成二进制去存,这就产生了不能精确的存储数的问题。同时有两个技巧也值得注意,第一个就是用存储指数的时候,我们用正数表示负数。第二个就是,默认规定最高位是1,从而用23个比特位存了24位的数据。
