准备写一篇关于浮点数存储的，然后先写了进制转换，越写越多，就单独作为一篇文章吧。

2019.723，这个数的二进制形式是什么样呢？让我们慢慢考虑。

数字的概念

首先思考一下数字是什么？为什么要有数字。

我有一个苹果，你脑海中会出现一个苹果。

我有五个苹果，你脑海中会出现五个苹果。

我有三十个苹果，你脑海中会出现三十个苹果。

我有一千个苹果，你可能想象不出来了。

数字的作用，就是让我们对一个东西的数量有一个更精确的认识。如果没有数字，我可能只能说我有一桌子苹果，我有一堆苹果，我有一大堆苹果，我有一大大堆苹果，这些都是感性的认知，每个人的认知可能是不一样的，而数字统一了我们对「量」的概念。

此外，另一个神奇的地方在于数字仅仅是「量」的概念，他没有限制去描述什么。

比如说五个苹果，五只小狗，五头牛，五粒大米，数量都是五，但他们的体积、质量、形状都和他们本身有关了。

数字的记录

后来人类发明了纸笔，如果把这个「量」的概念写下来该怎么办呢？

最简单的想法就是画竖线，每增加一个，就加一条竖线。

1 -> I

2 -> II

3 -> III

4 -> IIII

5 -> IIIII

20 -> ???

如果数字大了，一直画竖线显然是不现实的，在出土的甲骨文中发现了当时人们对数字的认识。

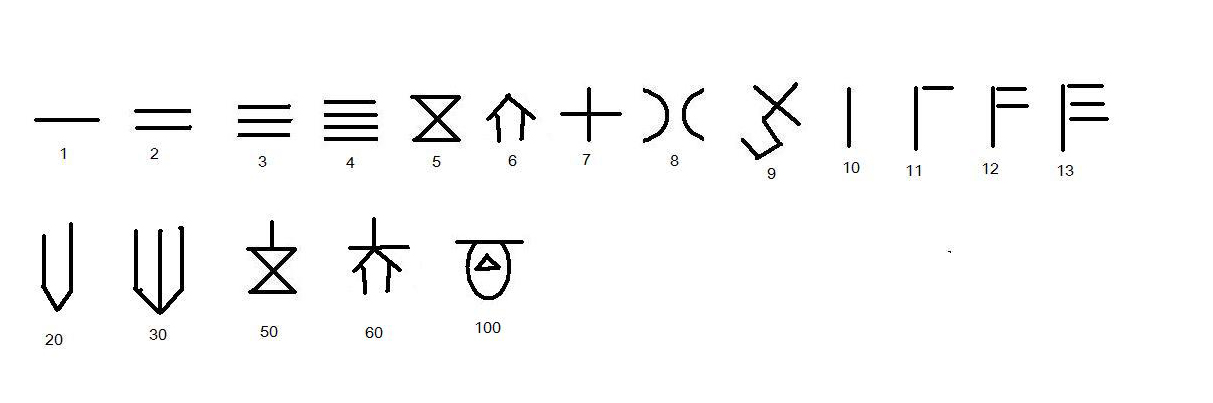
一些大的数字用一些特定的符号来表示，这样如果表示 108 的话，我们只需要画出这两个图形就可以了。

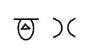
顺序无所谓，另一个人可能画出的是下边的

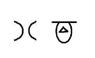
即使顺序不一样，但他们表示的数字都是 108。

进制的概念

上边的依旧不是很方便，比如我要是想表示 1000，如果我们只有 100 对应的符号，我还是需要画 10 个才行。接下来，人们用了一个更伟大的发明，进位制，也许因为人有 10 根手指，所以采用了 10 进制，其实就是我们现在的计数法。用0 - 9 十个符号就可以表示任意数字了。

这里边最伟大的发明就是0的概念了，它除了表示数量上的 0，也可以用来占位。从而数字在不同的位置有了不同的含义。拿十进制来举例，就是逢十进一。

得到一个苹果，写个 1，得到六个苹果，写个6，得到十个苹果了，怎么表达十这个数量呢，低位用0占位，高位写1就可以了。也就是10。此时的1不再是一，而是一个十。同理100，就表明有十个十的数量。此外再发明一个小数点，0.1，小数点右边的一表明是十分之一。

每个位置就有了不同的含义，可以看作下边的公式。e 是小数点后开始的数位。

$$…+a\times10^3+b\times10^2+c\times10^1+d\times10^0+e\times10^{-1}+f\times10^{-2}+g\times10^{-3}+…$$

a，b，c … 代表0 - 9中的任意一个符号，现在的数量是a个1000，b 个 100，c 个 10……

比如2019.723就可以看成下边的样子

$$2\times10^3+0\times10^2+1\times10^1+9\times10^0+7\times10^{-1}+2\times10^{-2}+3\times10^{-3}$$

上边是十进制，让我们想一下 2 进制。

2 进制只有两个符号可以用，那就是0和 1，规则是满2 就要进 1。

如果有一个苹果那么就记做1，如果有两个苹果要利用0来占位，高位写1，也就是10，如果有四个苹果，那就用100来表示。

因为我们对十进制太熟悉了，如果我说「我考了100分」。大家第一反应就是我考的不错，但如果是在二进制的世界，100其实是一个蛮小的数字。

如果把二进制换两个符号，比如>来表示一个苹果，<来表示零的概念，用来占位。我如果说我考了><<分，这样大家就没有条件反射觉得我考的很高了。

所以我们要明确一个概念，不同进制下，可能用了同一个符号，但对于同一个数量，那么表示法是不一样的。

看到这么多苹果，

商朝人可能会写下，我有| 二个苹果。

十进制的人们会写下，我有 12 个苹果。

二进制的人们会写下，我有 1100 个苹果。

可以看到对于同一个数量，大家的表示是不一样的，即使十进制和二进制的人们用了相同的符号0和1，但由于进制不同，他们写出来是不一样的。

有一天二进制的人和十进制的人相遇了，二进制的人说，我买了1100个苹果，然后对于十进制的人第一反应，哇，一千多个苹果，也太多了吧。

二进制的人们，看到1100立马脑海中联想到了上图的数量，但是对于十进制人们必须把这个数量转换成自己熟悉的十进制表示，才可以在脑海里想象1100个苹果的数量是多少。那么怎么转换呢？

二进制转十进制

让我们从十进制的角度去看一下二进制，二进制是满二进一，所以他的每一位的权重其实是以 2 为权重的，就是下边的样子。

$$…+a\times2^3+b\times2^2+c\times2^1+d\times2^0+e\times2^{-1}+f\times2^{-2}+g\times2^{-3}+…$$

a，b，c … 代表0和 1中的一个，现在的数量是 a 个 8，b 个 4，c 个 2 ……

所以1100如果用十进制表示，就是 1 个 8 加上 1 个 4，也就是12了。这样的话，我们就可以理解他买了多少苹果了。

十进制转二进制

那么十进制怎么转换成二进制呢？最开始的问题，怎么用二进制去表示 2019.723。

整数的转换

其实这就是数学上的问题了，首先我们考虑整数部分2019。根据前边二进制转十进制的公式，我们知道可以有下边的等式。

$$…a\times2^4+b\times2^3+c\times2^2+d\times2^1+e\times2^0=2019$$

两边如果同时除以 2 会发生什么呢，

$$…a\times2^3+b\times2^2+c\times2^1+d\times2^0+e/2=2018/2+1/2$$

可以看到系数是 a，b，c，d的部分都整除了，只剩下 e/2。

右边的话，把2019分成两部分2018和1。然后就是$2018/2$和$1/2$两部分。

左边也看做$…a\times2^3+b\times2^2+c\times2^1+d\times2^0$和$e/2$两部分。

左右两部分对应相等。

右边的部分。

$$e/2==1/2$$

所以算出了 $e=1$。

再看左边的部分。

$$…a\times2^3+b\times2^2+c\times2^1+d\times2^0=2018/2=1009$$

我们可以两边继续同时除以2，就可以求出d。同理就可以求出a，b，c以及更多的系数。

再来回想一下我们的方法，两边同时除以2，然后被分成$2018/2$和$1/2$两部分，其实左边就是商，右边是余数。2019/2=1009······1，对应等式左边的部分，e 其实就等于余数。

所以转换的方法就是用2019除以2，余数作为二进制的低位。商作为新的除数，继续除以2，余数作为二进制的低位…直到商为 0。

因为我们每次求出的都是二进制对应的低位，书写的话习惯于先写高位，所以倒着写过来 11111100011就是2019的二进制形式了。

写成代码的形式。

public static List<Integer> integerTrans(int n) {
    ArrayList<Integer> list = new ArrayList<>();
    while (n != 0) {
        list.add(n % 2);
        n /= 2;
    }
    for (int i = list.size() - 1; i >= 0; i--) {
        System.out.print(list.get(i));
    }
    return list;
}

小数的转换

考虑完整数，再来想一下小数0.723怎么处理。同样的，利用二进制转十进制的公式，写出下边的等式。

$$e\times2^{-1}+f\times2^{-2}+g\times2^{-3}+…=0.723$$

之前同时是利用两边同时除以2，对于上边的等式肯定不行了。换一下，两边同时乘以2呢？看看会发生什么。

$$e\times2^{0}+f\times2^{-1}+g\times2^{-2}+…=0.723\times2$$

和之前一样，把两边分别分成两部分。

$$e+f\times2^{-1}+g\times2^{-2}+…=1+0.446$$

两部分分别对应相等，可以知道

$$e==1$$

另外一部分的话

$$f\times2^{-1}+g\times2^{-2}+…=0.446$$

我们继续同时乘以2，变成下边的样子。

$$f+g\times2^{-1}+…=0 + 0.892$$

这样又可以求出$f=0$，同样的一直不停的继续下去，直到得到的新的小数部分是0。

所以我们的算法就是不停的乘2取整数部分，有可能得到的新的数永远不等于 0，这就取决于我们需要的精度了，可以随时停止。

小数的话正着写出来就可以了，0.1011就是十进制0.723的近似值了。

所以十进制小数转成二进制并不会像十进制整数那么顺利。原因的话，因为二进制小数它的权重依次是0.5,0.25,0.125…，所以只有这些数的任意相加才能被精确表示。大部分的十进制小数都不能精确的用二进制表示。

甚至看起来最简单的0.1如果转成二进制，会是什么样呢？

可以看到计算过程中，出现了循环，0.4，0.8，0.6，0.2会循环出现，所以0.1的二进制表示就是0.0 0011 0011 0011...是一个无限循环小数了。它就相当于我们十进制中的1/3，写成小数形式是0.3333333...。

用代码表示一下，我们只保留 10 位小数。

public static List<Integer> decimalTrans(double n) {
    ArrayList<Integer> list = new ArrayList<>();
    int count = 10;
    while (count > 0) {
        n = n * 2;
        list.add((int) (n));
        n = n - (int) (n);
        count--;
    }
    for (int i = 0; i < list.size(); i++) {
        System.out.print(list.get(i));
    }
    return list;
}

历史的发展

可以看一下现实生活中数字的发展，引自维基百科。

无位值十进制

古埃及十进制：以一个竖道代表1，二并排竖道代表2，三竖道代表3，一横道代表4，左二撇右竖道代表5，上三撇下三撇代表6，上下两道代表8，四个（并排代表9，一个“人”字形代表10，“人”上加一横代表20，20左加一点代表30，横道上加一点代表40，横道上加三竖道（如中国筹算的8）代表60，横道上加四竖道代表80（形同中国筹算中的9）代表80，两横道上加三竖代表90……。

古希腊十进制，1至9，10至90，100至900各有不同的单字母代表。

古印度Kharosshi十进制，以一个竖道代表1，二并排竖道代表2，三竖道代表3，一个X代表4，IX代表5，||X代表6，XX代表8，10，20个有单字符代表。

古印度和Brahmi十进制，和希腊十进制相似，1至9，10至90，100至900各有不同的单字母代表。符号很多。

非十进的进位制

巴比伦60进位制：以一个上大下小的楔形代表1，两个并列楔形代表2，三个并列楔形代表3，上二个楔形下二个楔形代表4，上三楔下二楔代表5，上三楔下三楔代表6，上四楔下三楔代表7，上四楔下四楔代表8，上五楔下四楔代表9；一个左小右大横楔代10，两个横楔并排代表20，三个横楔并排代表30，四个横楔并排代表40。

玛雅20进位制：以一个点代表1，两个点并列代表2，三点并列代表3，四点并列代表4，短横线代表5，横线上加一点代表6，横线上加二点代表7，横线上加三点代表8，横线上加四点代表9；上下两横线代表10，上下两横线之上加一点代表11，三重叠横线代表15，三横线上加一，二，三点代表16，17，18；小椭圆圈上加一点代表20。

十进位制

中国古代的十进制有书写式和算筹两种型式。

印度-阿拉伯十进位制。

结束

不得不感慨下人类的聪明，将量的概念抽象出来，不同地区的独立发展，最后又是那么的相像。所以数字，其实就是符号对数量的映射，并且人们达成了共识。