Gradient Descent 美[ˈɡrediənt] [dɪˈsɛnt] : 梯度下降
Loss funcition 美 [lɔs] [ˈfʌŋkʃən] : 损失函数
Local Minima 美 [ˈloʊkl] [‘mɪnɪmə] : 局部最小值
Taylor series 美[ˈtelɚ] [ˈsɪriz] : 泰勒级数
本文是对李宏毅教授课程的笔记加上自己的理解重新组织,如有错误,感谢指出。
视频及 PPT 原教程:https://pan.baidu.com/s/1bSs66a 密码:g8e4
上篇线性回归讲到, $ L = \sum_{n=0}^{10} ( \hat{y}^n - ( b+ w · x{^n_{cp}} ) )^2$ 这个模型中,我们穷举了 w 和 b 的值,然后找到了使得 L 最小的 w 和 b 的值,但对于参数较多的模型,穷举法显然是不合适的,这里我们将用到 Gradient Descent,而 Gradient Descent 这个方法不仅适用于线性回归,其他任何复杂的模型也都适用,就连深度学习也用的 Gradient Descent 。
我们人类只能想象出最高三维空间的场景,所以我们先在二维、三维空间形象的理解下 Gradient Descent ,然后直接把结论推广到高维下,这里不做详细的理论证明。
一维变量
一维变量下,变量只能在一条直线上移动,向左或向右。
假设 Loss funcition 是有一个参数 w 的函数,例如
$$L = sin(w) + w^4 + w + log(w)+x_i$$
$x_i$是要输入的数据特征,例如上篇的 cp 值,可以看做常量。
而它的图像假如是
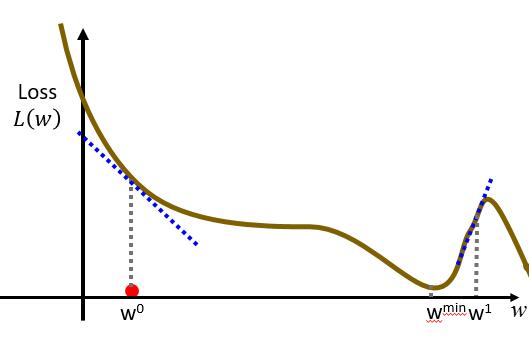
从图像上可以看到我们要找的使得 Loss 值最小的就是 $w^{min}$
我们如果开始选取的是 $w^0$ ,那么我们需要给 $w^0$ 加上一个值可以得到 $w^{min}$ 。
我们如果开始选取的是 $w^1$ ,那么我们需要给 $w^1$ 减去一个值可以得到 $w^{min}$ 。
至于是加上还是减去,我们可以观察到,当 w 的斜率为负的时候就加,斜率为正的时候就减。斜率等于 0 的时候就代表是一个最小值点了。
所以我们可以先把 w 随便取一个值 $w^0$ ,然后求出该点的斜率,也就是 $w^0$ 的导数值 $\frac{dL}{dw}|_{w=w^0}$ ,然后用 $w^0$ 减去这个导数值乘以一个 $\eta$ ,叫做 learning rate ,就是控制它从 $w^0$ 走到 $w^{min}$ 的速度。为什么是减去呢,因为斜率的符号和要加还是要减刚好是反着的。就是下边的数学表达式
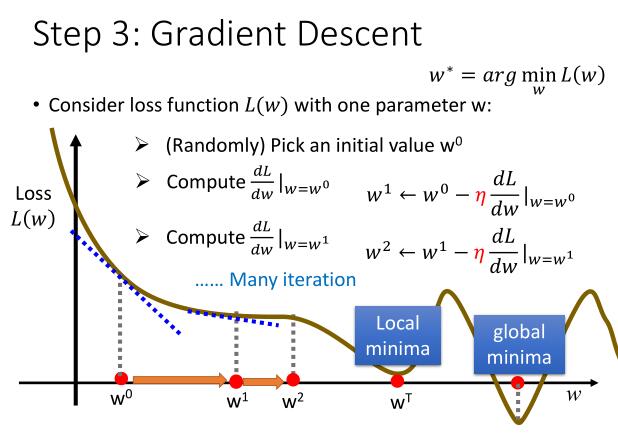
根据 $w_0$ 得到 $w_1$ ,再根据 $w_1$ 得到 $w_2$,一直迭代,直到使得 Loss 值最小,当然从图上就可以看到我们可能会到达一个 Local minima ,也就是局部最小,后边再讲这个问题。而线性回归不需要考虑这个问题,因为它如果有极小值,那么这个极小值一定是最小值。
二维变量
二维变量下,变量则可以在整个平面上移动。
我们再看一下 Loss function 有两个变量的情况,例如
$$L = \theta_1 · x_1 + \theta_2 · x_2$$
假如它的分布图如下,利用等高线画出来的,可以想象成盆地的等高线,颜色浅代表是底部:
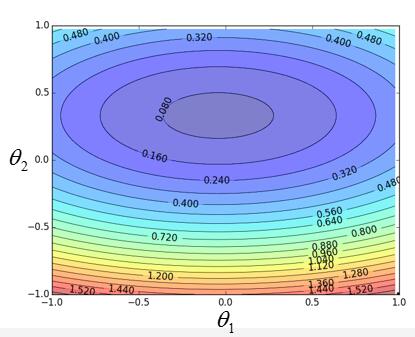
Taylor series
在数学中,泰勒级数(英语:Taylor series)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(Sir Brook Taylor)来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数,以苏格兰数学家科林·麦克劳林的名字命名。 –维基百科

只要 x 足够接近 $x_0$ ,我们可以近似的取到 h 的一阶导数,后边将用到这个公式。
Multivariable Taylor Series
同理,可以推广到多元的泰勒展开。
分别对自变量求偏导即可。
推导
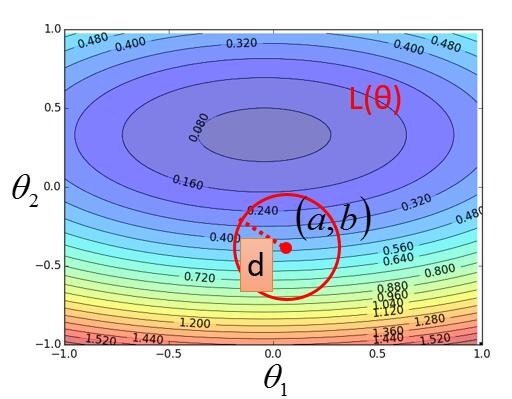
假设开始我们初始化 $ \theta_1 = a$ , $ \theta_2 = b$ ,然后以 d 为半径画一个很小很小的圆,以便满足泰勒级数中的那个约等于的式子(图上圆看着大,我们假设它很小)。然后我们在这个圆里寻找使得 Loss 值最小的 $\theta_1$ 和 $\theta_2$ 。得到新的$\theta_1$ 和 $\theta_2$ ,继续重复画一个圆,找使得圆内 Loss 值最小的 $\theta_1$ 和 $\theta_2$ ,然后一直迭代下去,慢慢的我们就会得到使得 loss 值全局最小的 $\theta_1$ 和 $\theta_2$ 了。
那么,怎么根据已知的点,找到下一个点呢?下边进行一下推导
将 L 利用泰勒级数转换。
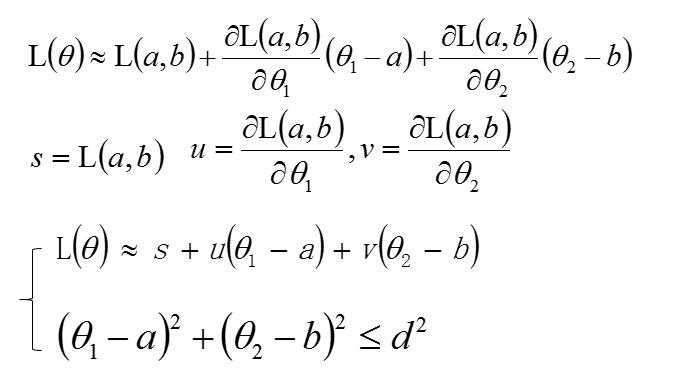
将问题利用转换为几何问题
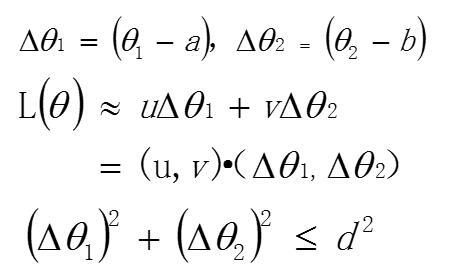
我们把 L 看做是两个向量的点积,(u,v) 向量是一个固定的向量 ,我们把它的起点移动到圆心 的位置。而 $(\Delta\theta_1 , \Delta\theta_2) $ 向量是任意方向的,长度小于 d 的向量,为了方便计算,我们把它的起点也移动到圆心的位置。
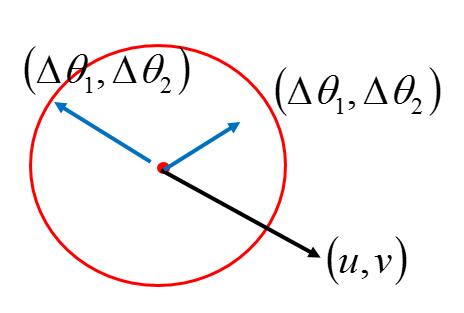
我们知道两个向量点积的公式
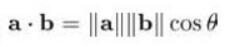
所以我们取 $(\Delta\theta_1 , \Delta\theta_2) $ 向量为 &(u,v)&向量的反向,构成 180° ,使得 $cos\theta$ 等于 -1 ,然后使得它的模最大,也就是 d (乘上 $\eta$ 即可),此时 L 由于是他俩的点积,所以 L 达到最小。即
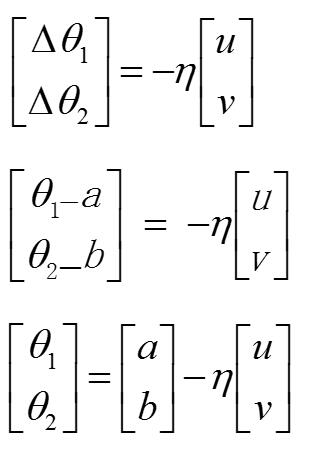
然后我们再把 u 和 v 带回去
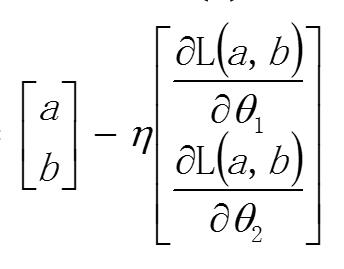
!!! 和一维变量一样,就是初始值,减去 $\eta$ 乘以他们的导数,但这里当然是偏导了。这样再回到开头,我们就先随便找一个初始值 (a , b),利用这个公式然后一直迭代下去就可以了。
总
我们把两种情况统一下
也就是找一组参数 $\theta^*$ ,然后使得 Loss function L 取得最小值,即用数学表达式为

我们假设 $\theta$ 有两个参数 ${\theta_1 , \theta_2}$
初始化 $\theta_0$
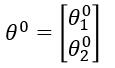
进行迭代
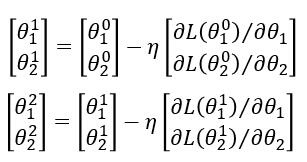
数学里那个大的中括号可以表示为倒三角,即梯度。我们进一步简化表示。
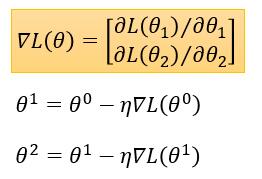
实例
回到我们开始的问题,直接应用上边的结论。
$$ L = \sum_{n=0}^{10} ( \hat{y}^n - ( b+ w · x{^n_{cp}} ) )^2$$
让我们把他们的偏导分别求一下
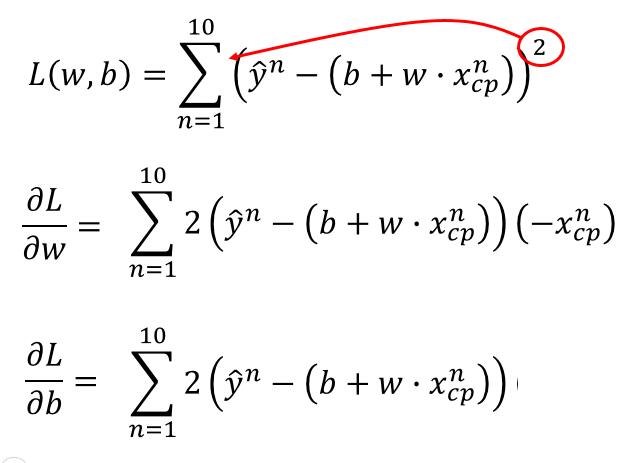
有了偏导的公式,我们只需要把 w 和 b 取一个初值,然后利用所有的数据和梯度下降,一直迭代下去就可以了。迭代次数、Loss 值、偏导值都可以作为结束条件。
至此,一大难题已经被我们解决了!!!!!!!!!!!

